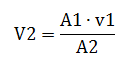En la materia de cálculo diferencial se abarcaron diversos conceptos importantes en el cálculo diferencial como es el de limite, que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.
O el de derivada que mide la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en cierto intervalo.
Estos conceptos y muchas más áreas de las matemáticas convergen al aplicar un modelo matemático a una problemática ambiental
Desde el enfoque de las matemáticas, como bien sabemos, nos permiten auxiliar a otras ciencias como la física, la química, biología, estadística, etc. Planteando sistemas abiertos o cerrados en los que comprender y predecir datos por medio de cálculos matemáticos, claramente podemos tomar algún sistema relacionado con nuestra problemática y aportar datos que nos permitan comprender la magnitud del problema en cuestión.
En nuestro caso, el problema es la contaminación de agua y sus repercusiones en sistemas de riego, drenaje y otros en los que se involucren tuberías, usando modelos matemáticos básicos de la hidrodinámica como la ecuación de flujo de fluidos, mejor conocida como principio de Bernoulli, podemos conocer repercusiones de la contaminación del agua en cañerías o drenajes.
Modelo matemático
En dinámica de fluidos, el principio de Bernoulli, también denominado ecuación de Bernoulli o trinomio de Bernoulli, describe el comportamiento de un líquido moviéndose a lo largo de una corriente de agua. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido.
Enunciado se expresa:
“dentro de un flujo horizontal de fluido, los puntos de mayor velocidad del fluido tendrán menor presión que los de menor velocidad.”
Inicialmente, en su obra Bernoulli expresó su ecuación como una equivalencia entre distintos tipos de energías en un fluido.
Sin embargo, intuitivamente, la ecuación de Bernoulli explica una equivalencia en la energía del fluido en distintas partes de la tubería, implicando que una reducción en el diámetro de una tubería se compensa aumentando la velocidad del fluido en su interior
La ecuación de Bernoulli relaciona la presión, la velocidad y la altura de dos puntos cualesquiera (1 y 2) en un fluido con flujo laminar constante de densidad. Usualmente se escribe la ecuación de Bernoulli de la siguiente manera:
Ec1+Ep1+EP1=Ec2+Ep2+EP2
Donde:
Ec=Energía cinética del fluido
Ep=Energía potencial del fluido
EP=Energía de presión
Cuyas fórmulas para cada energía son:
Ec=mv12
Ec= Energía cinética
m=Masa del líquido
v=Velocidad del fluido
Ep=mgh
Ep= Energía potencial
m=Masa del líquido
g=Aceleración gravitatoria
EP=Pm
EP= Energía de presión
P=Presión ejercida por el fluido
m=Masa del líquido
=Densidad del fluido
Finalmente, sustituyendo estas fórmulas en la ecuación inicial nos queda:
Aplicación
Despejes en esta ecuación nos permiten conocer ciertos datos del modelo en el que se está trabajando, por ejemplo:
Para conocer el diámetro de la tubería en un segundo punto teniendo uno ya:
Para conocer la velocidad que lleva el fluido en un segundo punto teniendo uno ya:
O para conocer la presión en un segundo punto teniendo uno ya:
Por lo tanto, un caso por ejemplo cuya densidad fuera alta, el fluido perdería velocidad y aumentaría la presión en esa zona
Otro dato importante que nos da la ecuación de Bernoulli es que en un rio, por ejemplo el fluido más denso como es el caso del agua contaminada por residuos líquidos domésticos o químicos industriales, fluiría más lento e incluso cabría la posibilidad de que en estrechamientos del río, este se atascara completamente, y si el flujo es constante, podría incluso desbordarse.
Graficamente, este es el comportamiento que sigue la presión en un fluido modelo (densidad igual o muy similar a la del agua)
Gráficamente este es el comportamiento que suele seguir la velocidad del agua en un fluido modelo (densidad igual o muy similar a la del agua)